备战前端面试–数据结构与算法篇
前言
不同于其他知识,数据结构与算法在温习理论的同时,必须结合实战。只有经过日积月累的训练,才能有可观的提升。
如何刷?根据自己的薄弱知识点,定向刷相应的专题。如果时间多,按简单到困难的顺序刷完也可以。
必要的算法,如果写不熟练,建议全文背诵bushi。
本文仅用于记录个人在力扣刷题的过程。
栈
简介
一个后进先出的数据结构
JS 版本实现:
在 JS 中,通常用 Array 来模拟栈。
let stack = []
stack.push(0)// 入栈
stack.push(1)
stack.pop() // 出栈应用场景
十进制转二进制:
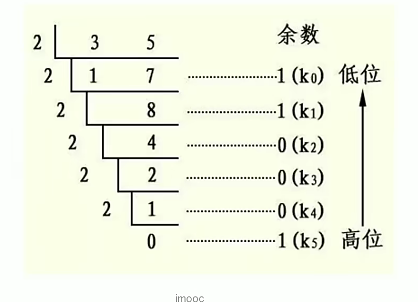
余数依次入栈,之后出栈,实现倒序输出。
函数调用堆栈:
JS 解释器使用栈来控制函数调用顺序。函数中调用函数,对应入栈过程。函数退出,对应出栈过程。递归就是利用了函数调用栈特性,最后调用的函数先执行完,其实际的空间复杂度为 O(n)。所以做题的时候,记得计算递归的空间复杂度。
做题环节
LeetCode 20. 有效的括号
给定一个只包括 ‘(‘,’)’,’{‘,’}’,’[‘,’]’ 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
示例 :
输入:s = "()"
输出:true
输入:s = "()[]{}"
输出:true
输入:s = "(]"
输出:false
输入:s = "([)]"
输出:false
输入:s = "{[]}"
输出:true通过观察可发现,对于没有闭合的左括号而言,越靠后的左括号,其右括号越靠前。满足后进先出。所以首先应该想到用栈来解题,思路如下:
- 如果输入字符串长度为奇数,直接判断不合法
- 新建一个栈
- 扫描字符串,遇左括号,将其匹配的右括号入栈
- 遇到右括号执行一次出栈和栈顶匹配,不匹配直接返回 false
- 最后检测栈为空则合法
/**
* @param {string} s
* @return {boolean}
*/
var isValid = function (s) {
if (s.length % 2 !== 0) return false
const stack = []
for (let i = 0; i < s.length; i++) {
const c = s[i]
switch (c) {
case "(":
stack.push(")")
break
case "{":
stack.push("}")
break
case "[":
stack.push("]")
break
default:
if (stack.pop() != c) return false
}
}
return stack.length === 0
};LeetCode 155. 最小栈
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
push(x) —— 将元素 x 推入栈中。
pop() —— 删除栈顶的元素。
top() —— 获取栈顶元素。
getMin() —— 检索栈中的最小元素。
输入:
["MinStack","push","push","push","getMin","pop","top","getMin"]
[[],[-2],[0],[-3],[],[],[],[]]
输出:
[null,null,null,null,-3,null,0,-2]
解释:
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); --> 返回 -3.
minStack.pop();
minStack.top(); --> 返回 0.
minStack.getMin(); --> 返回 -2.分清题意,本题并非让我们手动实现栈的相应方法,相应的,只需要确保我们指定函数能完成其功能。比较麻烦的是在常数时间内检索到最小元素。这说明,我们绝不能在需要最小值的时候,再做排序,查找等操作来获取。因此,我们可以创建两个栈,一个栈是主栈 stack,另一个是辅助栈 minStack,用于存放对应主栈不同时期的最小值。思路如下:
- 创建两个栈,主栈 stack,辅助栈 minStack
- push 操作,主栈直接入栈,辅助栈将当前值与其栈顶比较,然后决定是否入栈
- pop 操作,同时将主栈和辅助栈中的栈顶元素出栈
- top 操作,返回主栈的栈顶元素
- getMin 操作,返回辅助栈的栈顶元素
var MinStack = function() {
this.x_stack = [];
this.min_stack = [Infinity];
};
MinStack.prototype.push = function(x) {
this.x_stack.push(x);
this.min_stack.push(Math.min(this.min_stack[this.min_stack.length - 1], x));
};
MinStack.prototype.pop = function() {
this.x_stack.pop();
this.min_stack.pop();
};
MinStack.prototype.top = function() {
return this.x_stack[this.x_stack.length - 1];
};
MinStack.prototype.getMin = function() {
return this.min_stack[this.min_stack.length - 1];
};LeetCode 224. 基本计算器
给你一个字符串表达式
s,请你实现一个基本计算器来计算并返回它的值。
输入:s = "1 + 1"
输出:2
输入:s = " 2-1 + 2 "
输出:3
输入:s = "(1+(4+5+2)-3)+(6+8)"
输出:23简单的困难题,毕竟小学就学过了加减法运算,优先计算嵌套最深的括号内的表达式。观察可知,越靠后的左括号,其匹配的右括号越靠前。并且每当遇到匹配的右括号,就计算当前括号内表达式的值,然后与外部的左表达式进行加减运算。用一个栈来存储运算符和之前的表达式值,思路还是比较清晰的:
- 创建栈 stack,当前值 num,累加值 res,系数 sign
- 依次取出字符串中不为运算符的值,赋值给 num
- 每次遇到运算符之前,让
res += num * sign - 加减运算符,改变下一次运算的系数
- 左括号运算符,把当前累加值和系数入栈,同时初始化
- 右括号运算符,出栈得到之前的累加值和系数
/**
* @param {string} s
* @return {number}
*/
var calculate = function (s) {
s = s.replace(/\s/g, '')
let len = s.length
let res = 0
let num = 0
let sign = 1
let stack = []
for (let i = 0; i < len; i++) {
if (s[i] >= 0 && s[i] <= 9) {
num = num * 10 + (s[i] - '0')
continue
}
// 当前 s[i] 为运算符,进行累加
res += num * sign
num = 0
if (isNaN(s[i]) || i == len - 1) {
switch (s[i]) {
case "(":
{
stack.push(res)
stack.push(sign)
// 初始化,重新开始计算
res = 0
sign = 1
break
}
case "+":
{
sign = 1
break
}
case "-":
{
sign = -1
break
}
case ")":
{
sign = stack.pop()
num = res // 当前括号内表达式的值
res = stack.pop() //括号外表达式的值
break
}
}
}
}
// 最后一项不再迭代,所以需要清算
res += num * sign
return res
};至于eval、Function 这种偷鸡方法不推荐,对成长没有任何帮助。
LeetCode 232. 用栈实现队列
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty):
实现 MyQueue 类:
void push(int x) 将元素 x 推到队列的末尾
int pop() 从队列的开头移除并返回元素
int peek() 返回队列开头的元素
boolean empty() 如果队列为空,返回 true ;否则,返回 false说明:
你只能使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
你所使用的语言也许不支持栈。你可以使用 list 或者 deque(双端队列)来模拟一个栈,只要是标准的栈操作即可。进阶:
你能否实现每个操作均摊时间复杂度为 O(1) 的队列?换句话说,执行 n 个操作的总时间复杂度为 O(n) ,即使其中一个操作可能花费较长时间。
示例:
输入:
["MyQueue", "push", "push", "peek", "pop", "empty"]
[[], [1], [2], [], [], []]
输出:
[null, null, null, 1, 1, false]
解释:
MyQueue myQueue = new MyQueue();
myQueue.push(1); // queue is: [1]
myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue)
myQueue.peek(); // return 1
myQueue.pop(); // return 1, queue is [2]
myQueue.empty(); // return false如果要满足进阶要求,就不能采用倾倒出来再倒回去的方式。因此可以把 A 作为辅助栈,B 作为输出栈,往 A 里 push 元素,当 B 为空时,就将 A 倒入 B,B 的栈尾即为队列的开头。
var MyQueue = function () {
this.stackA = []
this.stackB = []
};
/**
* @param {number} x
* @return {void}
*/
MyQueue.prototype.push = function (x) {
this.stackA.push(x)
};
/**
* @return {number}
*/
MyQueue.prototype.pop = function () {
this.A2B()
return this.stackB.pop()
};
/**
* @return {number}
*/
MyQueue.prototype.peek = function () {
this.A2B()
return this.stackB[this.stackB.length - 1]
};
/**
* @return {boolean}
*/
MyQueue.prototype.empty = function () {
if (!this.stackA.length && !this.stackB.length) return true
return false
};
MyQueue.prototype.A2B = function () {
if (!this.stackB.length) {
while (this.stackA.length) this.stackB.push(this.stackA.pop())
}
}剑指 Offer 31. 栈的压入、弹出序列
输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如,序列 {1,2,3,4,5} 是某栈的压栈序列,序列 {4,5,3,2,1} 是该压栈序列对应的一个弹出序列,但 {4,3,5,1,2} 就不可能是该压栈序列的弹出序列。
示例 1:
输入:pushed = [1,2,3,4,5], popped = [4,5,3,2,1]
输出:true
解释:我们可以按以下顺序执行:
push(1), push(2), push(3), push(4), pop() -> 4,
push(5), pop() -> 5, pop() -> 3, pop() -> 2, pop() -> 1示例 2:
输入:pushed = [1,2,3,4,5], popped = [4,3,5,1,2]
输出:false
解释:1 不能在 2 之前弹出。还是利用辅助栈,依次模拟入栈和出栈操作,如果结束后辅助栈仍非空,就判断不合法。
var validateStackSequences = function (pushed, popped) {
const stack = []
let i = 0
for (let num of pushed) {
stack.push(num)
while (stack.length && stack[stack.length - 1] === popped[i]) {
stack.pop()
i++
}
}
return !stack.length
};队列
简介
一个先进先出的数据结构。
JS 版本实现:
let queue = []
queue.push(0)// 入队
queue.push(1)
queue.shift() // 出队应用场景
事件循环
JS 的事件循环就是用的任务队列。在每次宏任务中,会把 then 的回调函数依次放入微任务队列,结束当前宏任务后依次执行。
并发请求控制
通过队列实现最大并发请求,每个请求的结束意味着另一个请求的入队。
做题环节
LeetCode 933. 最近的请求次数
写一个 RecentCounter 类来计算特定时间范围内最近的请求。
请你实现 RecentCounter 类:
RecentCounter() 初始化计数器,请求数为 0 。
int ping(int t) 在时间 t 添加一个新请求,其中 t 表示以毫秒为单位的某个时间,并返回过去 3000 毫秒内发生的所有请求数(包括新请求)。确切地说,返回在 [t-3000, t] 内发生的请求数。
保证 每次对 ping 的调用都使用比之前更大的 t 值。
示例:
输入:
["RecentCounter", "ping", "ping", "ping", "ping"]
[[], [1], [100], [3001], [3002]]
输出:
[null, 1, 2, 3, 3]
解释:
RecentCounter recentCounter = new RecentCounter();
recentCounter.ping(1); // requests = [1],范围是 [-2999,1],返回 1
recentCounter.ping(100); // requests = [1, 100],范围是 [-2900,100],返回 2
recentCounter.ping(3001); // requests = [1, 100, 3001],范围是 [1,3001],返回 3
recentCounter.ping(3002); // requests = [1, 100, 3001, 3002],范围是 [2,3002],返回 3利用队列先进先出特性,每次添加请求,将 3000ms 前的所有请求踢出队列。
RecentCounter.prototype.ping = function (t) {
this.queue.push(t)
while(this.queue[0] < t - 3000) this.queue.shift()
return this.queue.length
};LeetCode 225. 用队列实现栈
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)。
实现 MyStack 类:
void push(int x) 将元素 x 压入栈顶。
int pop() 移除并返回栈顶元素。
int top() 返回栈顶元素。
boolean empty() 如果栈是空的,返回 true ;否则,返回 false 。注意:
你只能使用队列的基本操作 —— 也就是 push to back、peek/pop from front、size 和 is empty 这些操作。
你所使用的语言也许不支持队列。 你可以使用 list (列表)或者 deque(双端队列)来模拟一个队列 , 只要是标准的队列操作即可。
示例:
输入:
["MyStack", "push", "push", "top", "pop", "empty"]
[[], [1], [2], [], [], []]
输出:
[null, null, null, 2, 2, false]
解释:
MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.top(); // 返回 2
myStack.pop(); // 返回 2
myStack.empty(); // 返回 False难点主要是 pop() 和 top() 的实现。pop 要得到队尾的元素,那么可以一直执行出队操作,直到剩下一个元素。暂时把出队的所有元素存储在另一个队列,取出队尾元素后再 push 回来。
var MyStack = function () {
this.queueA = []
this.queueB = []
};
/**
* @param {number} x
* @return {void}
*/
MyStack.prototype.push = function (x) {
this.queueA.push(x)
};
/**
* @return {number}
*/
MyStack.prototype.pop = function () {
while (this.queueA.length > 1) {
this.queueB.push(this.queueA.shift())
}
let res = this.queueA.shift()
while (this.queueB.length) {
this.queueA.push(this.queueB.shift())
}
return res
};
/**
* @return {number}
*/
MyStack.prototype.top = function () {
return this.queueA[this.queueA.length - 1]
};
/**
* @return {boolean}
*/
MyStack.prototype.empty = function () {
return !this.queueA.length
};LeetCode 239. 滑动窗口最大值
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回滑动窗口中的最大值。
示例 1:
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3
输出:[3,3,5,5,6,7]
解释:
滑动窗口的位置 最大值
--------------- -----
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7典型的双端队列问题。可以建立一个双端队列,当移动完成时,就执行一次出队,同时 push 进来一个新元素,如果为最大,就删除所有比它小的元素。这样每次双端队列的队首就是最大项,并且双端队列中的元素不断淘汰,显著降低时间复杂度。
var maxSlidingWindow = function (nums, k) {
if (nums.length === 0 || !k) return []
const window = []
const res = []
for (let i = 0; i < nums.length; i++) {
//每次窗口移动,队首出队
if (window[0] != undefined && window[0] <= i - k) window.shift()
// 确保队首始终为最大项
while (nums[window[window.length - 1]] <= nums[i]) window.pop()
window.push(i)
if (i >= k - 1) res.push(nums[window[0]])
}
return res
};链表
简介
一种存储空间不连续的非顺序数据结构,通过指针串联在一起。
JS 版本实现:
class listNode {
constructor(val) {
this.val = val;
this.next = null;
}
}
let a = new listNode(1);
let b = new listNode(2);
a.next = b;应用场景
JS 中的原型链
JS 中对象可以通过 _proto_属性指向它的原型对象。构造函数可以通过 prototype 指向它的原型对象。
JSON 的读取
可以通过指针遍历获取 JSON 中嵌套的元素。
做题环节
LeetCode 237. 删除链表中的节点
请编写一个函数,使其可以删除某个链表中给定的(非末尾)节点。传入函数的唯一参数为 要被删除的节点
输入:head = [4,5,1,9], node = 5
输出:[4,1,9]
解释:给定你链表中值为 5 的第二个节点,那么在调用了你的函数之后,该链表应变为 4 -> 1 -> 9.
输入:head = [4,5,1,9], node = 1
输出:[4,5,9]
解释:给定你链表中值为 1 的第三个节点,那么在调用了你的函数之后,该链表应变为 4 -> 5 -> 9.想要删除链表中的节点,首先得获得该节点的前一个节点。本题中只给出了要删除的节点,故此方法不可行。换一个思路,可以将该节点的下一个节点赋值给当前节点,再删除下一个节点,整体前移,实现删除。
var deleteNode = function(node) {
node.val = node.next.val
node.next = node.next.next
};LeetCode 206. 反转链表
给你单链表的头节点
head,请你反转链表,并返回反转后的链表。
输入:head = [1,2,3,4,5]
输出:[5,4,3,2,1]
输入:head = [1,2]
输出:[2,1]双指针前后移动遍历链表时,将当前节点的 next 指针改为指向前一个节点。由于节点没有引用其前一个节点,因此必须事先存储其前一个节点。在更改引用之前,还需要存储后一个节点。最后返回新的头引用。
var reverseList = function (head) {
let l = null, r = head;
while (r) {
const temp = r.next
r.next = l
l = r
r = temp
}
return l
};LeetCode 2. 两数相加
给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。
请你将两个数相加,并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
输入:l1 = [2,4,3], l2 = [5,6,4]
输出:[7,0,8]
解释:342 + 465 = 807.
输入:l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出:[8,9,9,9,0,0,0,1]用指针遍历 l1,l2 链表,取出当前值相加。如果等于或超过 10,就向前进位。最后将每一位的结果拼接成新链表,如果还有进位,再追加到其末尾。
var addTwoNumbers = function (l1, l2) {
const l3 = new ListNode(0)
let p1 = l1
let p2 = l2
let p3 = l3
let carry = 0
while (p1 || p2) {
const v1 = p1 ? p1.val : 0
const v2 = p2 ? p2.val : 0
const v3 = v1 + v2 + carry
carry = Math.floor(v3 / 10)
p3.next = new ListNode(v3 % 10)
if (p1) p1 = p1.next
if (p2) p2 = p2.next
p3 = p3.next
}
if (carry) p3.next = new ListNode(carry)
return l3.next
};LeetCode 83. 删除排序链表中的重复元素
存在一个按升序排列的链表,给你这个链表的头节点
head,请你删除所有重复的元素,使每个元素 只出现一次 。返回同样按升序排列的结果链表。
输入:head = [1,1,2]
输出:[1,2]
输入:head = [1,1,2,3,3]
输出:[1,2,3]用指针遍历链表所有节点,如果当前节点和下一位相同,就删除下一位,否则继续。
var deleteDuplicates = function (head) {
let p = head
while (p && p.next) {
// 和后一个节点相同
if (p.val == p.next.val) {
// 删除后一个
p.next = p.next.next
}
// 不相同指针才后移
else p = p.next
}
return head
};LeetCode 141. 环形链表
给定一个链表,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
如果链表中存在环,则返回 true 。 否则,返回 false 。
进阶:
你能用 O(1)(即,常量)内存解决此问题吗?
输入:head = [3,2,0,-4], pos = 1
输出:true
解释:链表中有一个环,其尾部连接到第二个节点。
输入:head = [1], pos = -1
输出:false
解释:链表中没有环。可以使用快慢指针遍历链表,如果是循环链表,两个指针必定会重新相遇。
var hasCycle = function (head) {
let p1 = head
let p2 = head
while (p1 && p2 && p2.next) {
// 快慢指针遍历
p1 = p1.next
p2 = p2.next.next
// 相逢则成环
if (p1 === p2) return true
}
return false
};LeetCode 92. 反转链表 II
给你单链表的头指针 head 和两个整数 left 和 right ,其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点,返回 反转后的链表 。
输入:head = [1,2,3,4,5], left = 2, right = 4
输出:[1,4,3,2,5]
输入:head = [5], left = 1, right = 1
输出:[5]穿针引线法:使用三个指针变量 pre、curr、next 来记录反转的过程中需要的变量,它们的意义如下:
cur:指向待反转区域的第一个节点 left;
next:永远指向 cur 的下一个节点,循环过程中,cur 变化以后 next 会变化;
pre:永远指向待反转区域的第一个节点 left 的前一个节点,在循环过程中不变。
var reverseBetween = function(head, left, right) {
const dummy = new ListNode(-1);
dummy.next = head;
let pre = dummy;
for (let i = 0; i < left - 1; ++i) {
pre = pre.next;
}
let cur = pre.next;
for (let i = 0; i < right - left; ++i) {
const next = cur.next;
cur.next = next.next;
next.next = pre.next;
pre.next = next;
}
return dummy.next;
};LeetCode 25. K 个一组翻转链表
给你一个链表,每 k 个节点一组进行翻转,请你返回翻转后的链表。
k 是一个正整数,它的值小于或等于链表的长度。
如果节点总数不是 k 的整数倍,那么请将最后剩余的节点保持原有顺序。
进阶:
你可以设计一个只使用常数额外空间的算法来解决此问题吗?
你不能只是单纯的改变节点内部的值,而是需要实际进行节点交换。
输入:head = [1,2,3,4,5], k = 2
输出:[2,1,4,3,5]
输入:head = [1,2,3,4,5], k = 3
输出:[3,2,1,4,5]
输入:head = [1,2,3,4,5], k = 1
输出:[1,2,3,4,5]递归法,简单粗暴,留一个头部节点用于拼接翻转后的节点:
const reverse = (a, b) => {
let pre, cur, nxt;
cur = a;
while (cur != b) {
nxt = cur.next;
cur.next = pre;
pre = cur;
cur = nxt;
}
// 返回反转后的头结点
return pre;
};
/**
* @param {ListNode} head
* @param {number} k
* @return {ListNode}
*/
var reverseKGroup = function (head, k) {
if (head == null) {
return head;
}
let a = head,
b = head;
for (let i = 0; i < k; i++) {
// 不足 k 个,不需要反转,base case
if (b == null) {
return head;
} else {
b = b.next;
}
}
// 反转前 k 个元素
let newHead = reverse(a, b);
a.next = reverseKGroup(b, k);
return newHead;
};常数空间的解法,断开和拼接的时机很关键,较难理解:
var reverseKGroup = function (head, k) {
const reverse = (head) => {
let pre, cur, nxt
cur = head
while (cur != null) {
nxt = cur.next
cur.next = pre
pre = cur
cur = nxt
}
return pre
}
if (!head) {
return head
}
const dummy = new ListNode(0)
dummy.next = head
let pre = dummy
let end = dummy
while (end.next != null) {
for (let i = 0; i < k && end; i++) {
end = end.next
}
if (end == null) break;
// 保存翻转头部节点的前驱节点
let start = pre.next;
// 保存翻转末尾节点的后继节点
let next = end.next
// 断开后继节点
end.next = null;
// 连接未翻转部分
pre.next = reverse(start)
start.next = next;
// 移动到下一个翻转区间
pre = start;
end = pre;
}
return dummy.next
};堆
二叉树
简介
是树形结构的一个重要类型,二叉树特点是每个结点最多只能有两棵子树,且有左右之分 。
JS 实现:
const bt = {
val: 1,
left: {
val: 2,
left: {
val: 3,
left: null,
right: null,
},
right: {
val: 4,
left: null,
right: null,
},
},
right: {
val: 5,
left: {
val: 6,
left: {
val: 7,
left: null,
right: null,
},
right: {
val: 8,
left: null,
right: null,
},
},
right: {
val: 9,
left: null,
right: null,
},
},
};做题环节
LeetCode 104. 二叉树的最大深度
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7]
3
/ \
9 20
/ \
15 7
返回它的最大深度 3 。深度优先遍历,途中记录当前的层级,使用递归实现。
var maxDepth = function (root) {
let count = 0
const dfs = (n, l) => {
if (!n) return
count = Math.max(l, count)
n.left && dfs(n.left, l + 1)
n.right && dfs(n.right, l + 1)
}
dfs(root, 1)
return count
};广度优先遍历,将当前层级的节点都遍历后,计数加一。
var maxDepth = function (root) {
let count = 0
const bfs = (n) => {
const q = [n]
while (q.length) {
let len = q.length
while (len) {
const cur = q.shift()
cur.left && q.push(cur.left)
cur.right && q.push(cur.right)
len--
}
count++
}
}
bfs(root)
return count
};LeetCode 111. 二叉树的最小深度
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
输入:root = [3,9,20,null,null,15,7]
输出:2
输入:root = [2,null,3,null,4,null,5,null,6]
输出:5广度优先遍历,适合求解此题,遇到叶子节点就可以直接返回了。
var minDepth = function (root) {
if (!root) { return 0 }
const bfs = (n) => {
let q = [[n, 1]]
while (q.length) {
let [n, l] = q.shift()
if (n.left) q.push([n.left, l + 1])
if (n.right) q.push([n.right, l + 1])
if (!n.left && !n.right) {
return l
}
}
}
return bfs(root)
};深度优先遍历,拿到所有节点再比较最小值即可。
LeetCode 102. 二叉树的层序遍历
给你一个二叉树,请你返回其按 层序遍历 得到的节点值。 (即逐层地,从左到右访问所有节点)。
二叉树:[3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回其层序遍历结果:
[
[3],
[9,20],
[15,7]
]广度优先遍历,把每层的所有访问结果推入一个数组中。
var levelOrder = function (root) {
if (!root) return []
const bfs = (n) => {
const q = [root]
let res = []
while (q.length) {
let len = q.length
res.push([])
while (len--) {
let n = q.shift()
res[res.length - 1].push(n.val)
if (n.left) q.push(n.left)
if (n.right) q.push(n.right)
}
}
return res
}
return bfs(root)
};LeetCode 94. 二叉树的中序遍历
给定一个二叉树的根节点
root,返回它的 中序 遍历。进阶: 递归算法很简单,你可以通过迭代算法完成吗?
输入:root = [1,null,2,3]
输出:[1,3,2]
输入:root = [1]
输出:[1]
输入:root = [1,2]
输出:[2,1]递归版本,遍历完所有左节点,就轮到根节点了。
var inorderTraversal = function (root) {
if (!root) return []
const res = []
const inorder = (n) => {
n.left && inorder(n.left)
res.push(n.val)
n.right && inorder(n.right)
}
inorder(root)
return res
};迭代版本,用栈来实现:
var inorderTraversal = function (root) {
if (!root) return []
const res = []
const stack = []
let p = root
while (stack.length || p) {
while (p) {
stack.push(p)
p = p.left
}
// 跳出说明已无左节点
const n = stack.pop()
res.push(n.val)
p = n.right
}
return res
};LeetCode 112. 路径总和
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum ,判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。
叶子节点 是指没有子节点的节点。
输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出:true
输入:root = [1,2,3], targetSum = 5
输出:false
输入:root = [1,2], targetSum = 0
输出:false此题适合用深度优先遍历。在遍历过程中记录当前节点的总和,只有在叶子节点处才返回。
var hasPathSum = function (root, targetSum) {
if (!root) return false
let res = false
const dfs = (n, s) => {
if (!n.left && !n.right && s === targetSum) {
res = true
}
if (n.left) dfs(n.left, s + n.left.val)
if (n.right) dfs(n.right, s + n.right.val)
}
dfs(root, root.val)
return res
};剑指 Offer 33. 二叉搜索树的后序遍历序列
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回
true,否则返回false。假设输入的数组的任意两个数字都互不相同。
参考以下这颗二叉搜索树:
5
/ \
2 6
/ \
1 3
输入: [1,6,3,2,5]
输出: false
输入: [1,3,2,6,5]
输出: true由于是二叉搜索树的后序遍历结果,数组最后一项就是根节点。根据定义,二叉搜索树的所有左节点都必须小于根节点,右节点必须大于根节点。根据这个来划分左右子树。
var verifyPostorder = function (postorder) {
let len = postorder.length;
// 若为叶子节点,则返回 true
if (len < 2) return true
// 后序遍历的最后一个元素为根节点
let root = postorder[len - 1];
let i = 0
// 划分左/右子树
for (; i < len - 1; i++) {
if (postorder[i] > root) break
}
// 判断右子树中的元素是否都大于 root,此处用到 every (数组 API,数组的每个元素都返回 true 则整体返回 true)
let result = postorder.slice(i, len - 1).every(x => x > root);
if (result) {
// 对左右子树进行递归调用,左右子树通过 i 进行分割
return verifyPostorder(postorder.slice(0, i)) && verifyPostorder(postorder.slice(i, len - 1))
} else {
return false
}
};图
排序和搜索
冒泡排序
介绍
思想:循环比较大小,依次交换,每次都把最大的元素冒泡到最右端。
时间复杂度 O(n^2),在所有排序中性能较差,因此不常用。
JS 实现
Array.prototype.bubbleSort = function () {
for (let i = 0; i < this.length - 1; i++) {
for (let j = 0; j < this.length - 1 - i; j++) {
if (this[j] > this[j + 1]) {
[this[j], this[j + 1]] = [this[j + 1], this[j]];
}
}
}
};选择排序
介绍
思想:依次找出数组中第一小、第二小…第 n 小的元素,放在数组的第一位、第二位…..第 n 位。
时间复杂度 O(n^2),同样性能较差。
JS 实现
Array.prototype.selectionSort = function () {
for (let i = 0; i < this.length - 1; i++) {
let minIndex = i;
for (let j = i; j < this.length; j++) {
if (this[j] < this[minIndex]) {
minIndex = j;
}
}
if (minIndex !== i) [this[i], this[minIndex]] = [this[minIndex], this[i]];
}
};插入排序
介绍
思想:从第二个元素开始,依次和之前的所有元素比较,更小则插入到其前面。
时间复杂度 O(n^2),数组长度小时性能较好。
JS 实现
Array.prototype.insertionSort = function () {
for (let i = 1; i < this.length; i++) {
const temp = this[i];
let j = i;
while (j > 0) {
if (this[j - 1] > temp) {
this[j] = this[j - 1];
} else break;
j--;
}
this[j] = temp;
}
};归并排序
介绍
思想:把数组拆分成两部分,再递归地对子数组拆分,直到分成单个的数。再把两个数合并为有序数组,对有序数组进行合并,直到形成完整的数组。
分的时间复杂度 O(log N),合的时间复杂度O(n),总时间复杂度 O(n*log N)。
JS 实现
左右双数组版本:
优点:思路简单,写法简单
缺点:空间复杂度略高,需要复制多个数组
Array.prototype.mergeSort = function () {
const rec = (arr) => {
if (arr.length <= 1) return arr;
const mid = Math.floor(arr.length / 2);
const left = arr.slice(0, mid);
const right = arr.slice(mid, arr.length);
const orderLeft = rec(left);
const orderRight = rec(right);
const res = [];
while (orderLeft.length || orderRight.length) {
if (orderLeft.length && orderRight.length) {
res.push(
orderLeft[0] < orderRight[0] ? orderLeft.shift() : orderRight.shift()
);
} else if (orderLeft.length) {
res.push(orderLeft.shift());
} else if (orderRight.length) {
res.push(orderRight.shift());
}
}
return res;
};
const res = rec(this);
res.forEach((n, i) => (this[i] = n));
};索引版本:
优点:空间复杂度低,只需一个temp存储空间,不需要拷贝数组
缺点:写法复杂
Array.prototype.mergeSort = function () {
const temp = [];
const rec = (arr, left, right, temp) => {
if (left < right) {
const mid = Math.floor((left + right) / 2);
rec(arr, left, mid, temp);
rec(arr, mid + 1, right, temp);
merge(arr, left, right, temp);
}
return arr;
};
function merge(arr, left, right, temp) {
const mid = Math.floor((left + right) / 2);
let leftIndex = left;
let rightIndex = mid + 1;
let tempIndex = 0;
while (leftIndex <= mid && rightIndex <= right) {
if (arr[leftIndex] < arr[rightIndex]) {
temp[tempIndex++] = arr[leftIndex++];
} else {
temp[tempIndex++] = arr[rightIndex++];
}
}
while (leftIndex <= mid) {
temp[tempIndex++] = arr[leftIndex++];
}
while (rightIndex <= right) {
temp[tempIndex++] = arr[rightIndex++];
}
tempIndex = 0;
for (let i = left; i <= right; i++) {
arr[i] = temp[tempIndex++];
}
}
rec(this, 0, this.length - 1, temp);
};快速排序
介绍
思想:从数组中随机选取一个基准值,将所有比它小的元素放在一边,把所有比它大的元素放在另一边,最后将基准元素插入它们的中间。递归对所有子数组进行同样的操作。
递归的时间复杂度 O(log N),分区的时间复杂度 O(n),总时间复杂度 O(n*log N)
JS 实现
Array.prototype.quickSort = function () {
const rec = (arr) => {
if (arr.length <= 1) return arr;
const left = [];
const right = [];
const mid = arr[0];
for (let i = 1; i < arr.length; i++) {
if (arr[i] < mid) {
left.push(arr[i]);
} else if (arr[i] > mid) {
right.push(arr[i]);
}
}
return [...rec(left), mid, ...rec(right)];
};
const res = rec(this);
res.forEach((n, i) => (this[i] = n));
};顺序搜索
介绍
遍历数组每一项,找出符合条件的元素。
时间复杂度 O(n)
JS 实现
Array.prototype.sequentialSearch = function (target) {
for (let i = 0; i < this.length; i++) {
if (this[i] === target) return i;
}
return -1;
};二分搜索
介绍
使用的前提是有序数组。每次都从中间开始搜索,没有找到就逐渐缩小搜索的范围。
时间复杂度 O(log N)
JS 实现
Array.prototype.binarySearch = function (target) {
let low = 0;
let high = this.length - 1;
while (low <= high) {
const mid = Math.floor((low + high) / 2);
if (this[mid] < target) {
low = mid + 1;
} else if (this[mid] > target) {
high = mid - 1;
} else {
return mid;
}
}
return -1;
};分治
介绍
思想:分而治之,把原问题拆分成多个和原问题相似的子问题,递归解决这些子问题,再把它们的结果整合,即为原问题的答案。
做题环节
LeetCode 374. 猜数字大小
猜数字游戏的规则如下:
每轮游戏,我都会从 1 到 n 随机选择一个数字。 请你猜选出的是哪个数字。
如果你猜错了,我会告诉你,你猜测的数字比我选出的数字是大了还是小了。
你可以通过调用一个预先定义好的接口 int guess(int num) 来获取猜测结果,返回值一共有 3 种可能的情况(-1,1 或 0):-1:我选出的数字比你猜的数字小 pick < num
1:我选出的数字比你猜的数字大 pick > num
0:我选出的数字和你猜的数字一样。恭喜!你猜对了!pick == num
返回我选出的数字。
示例 1:
输入:n = 10, pick = 6
输出:6示例 2:
输入:n = 1, pick = 1
输出:1这题可直接使用二分搜索来解,二分搜索其实就是一种分治的解法。
递归版:
空间复杂度较高,适合理解分治思想。
var guessNumber = function (n) {
const rec = (low, high) => {
if (low > high) return
const mid = Math.floor((low + high) / 2)
const res = guess(mid)
if (res === 0) {
return mid
} else if (res === -1) {
return rec(1, mid - 1)
} else {
return rec(mid + 1, high)
}
}
return rec(1, n)
};二分搜索版:
var guessNumber = function (n) {
let low = 1
let high = n
while (low <= high) {
const mid = Math.floor((low + high) / 2)
if (guess(mid) === 1) {
low = mid + 1
} else if (guess(mid) === -1) {
high = mid - 1
} else {
return mid
}
}
};LeetCode 100. 相同的树
给你两棵二叉树的根节点
p和q,编写一个函数来检验这两棵树是否相同。如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
输入:p = [1,2,3], q = [1,2,3]
输出:true
输入:p = [1,2], q = [1,null,2]
输出:false
输入:p = [1,2,1], q = [1,1,2]
输出:false递归比对根节点以及左右子树的值即可。
var isSameTree = function (p, q) {
if (!p && !q) return true
if (p && q && p.val === q.val && isSameTree(p.left, q.left) && isSameTree(p.right, q.right)) return true
else return false
};LeetCode 101. 对称二叉树
给定一个二叉树,检查它是否是镜像对称的。
例如,二叉树 [1,2,2,3,4,4,3] 是对称的。
1
/ \
2 2
/ \ / \
3 4 4 3但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:
1
/ \
2 2
\ \
3 3可看作一个分治问题,比较左右子树是否镜像。
分:获取两个树的左子树和右子树。
解:递归地判断树1的左子树和树2的右子树是否镜像,树1的右子树和树2的左子树是否镜像。
合:如果上述都成立,且根节点值也相同,两个树就镜像。
递归法:
var isSymmetric = function (root) {
if (!root) return true
const isMirror = (l, r) => {
if(!l && !r) return true
if (l && r && l.val === r.val &&
isMirror(l.left, r.right) &&
isMirror(l.right, r.left)
) return true
return false
}
return isMirror(root.left, root.right)
};迭代法:
var isSymmetric = function (root) {
if (!root) return true
const isMirror = (l, r) => {
const q = [l, r]
while (q.length) {
let u = q.shift()
let v = q.shift()
if (!u && !v) continue;
if (!u || !v || u.val !== v.val) return false;
q.push(u.left, v.right)
q.push(u.right, v.left)
}
return true
}
return isMirror(root.left, root.right)
};回溯
介绍
从解决问题每一步的所有可能选项里系统选择出一个可行的解决方案。
在某一步选择一个选项后,进入下一步,然后面临新的选项。重复选择,直至达到最终状态。
回溯法解决的问题的所有选项可以用树状结构表示。
- 在某一步有n个可能的选项,该步骤可看作树中一个节点。
- 节点每个选项看成节点连线,到达它的n个子节点。
- 叶节点对应终结状态。
- 叶节点满足约束条件,则为一个可行的解决方案。
- 叶节点不满足约束条件,回溯到上一个节点,并尝试其他叶子节点。
- 节点所有子节点均不满足条件,再回溯到上一个节点。
- 所有状态均不能满足条件,问题无解。
总结回溯的三要点:
选择,决定了搜索空间,决定了搜索空间有哪些节点。
约束,用来剪枝,避免进入无效的分支。
目标,决定了什么时候捕获有效的解,提前结束递归,开始回溯。
做题环节
LeetCode 46. 全排列
给定一个不含重复数字的数组
nums,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
示例 :
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
输入:nums = [0,1]
输出:[[0,1],[1,0]]
输入:nums = [1]
输出:[[1]]经典回溯入门级问题,递归找出所有可能的情况,注意处理重复。可以利用 forEach 的 return 无法中断循环这一特性来递归。
var permute = function (nums) {
const res = []
const backtrack = (path) => {
if (path.length === nums.length) {
res.push(path)
return
}
nums.forEach(n => {
if (path.includes(n)) return
backtrack(path.concat(n))
})
}
backtrack([])
return res
};LeetCode 78. 子集
给你一个整数数组
nums,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
输入:nums = [1,2,3]
输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
输入:nums = [0]
输出:[[],[0]]观察可得出,子集的长度一共有 nums.length 种(第一个例子中是 0 1 2 3)。那么可以用一个 for 循环,在里面递归找出所有符合当前长度的子集。
var subsets = function (nums) {
const res = []
const backtrack = (path, length, start) => {
if (path.length === length) {
res.push(path)
return
}
for (let i = start; i < nums.length; i++) {
backtrack(path.concat(nums[i]), length, i + 1)
}
}
for (let i = 0; i <= nums.length; i++) {
backtrack([], i, 0)
}
return res
};剑指 Offer 38. 字符串的排列
输入一个字符串,打印出该字符串中字符的所有排列。
你可以以任意顺序返回这个字符串数组,但里面不能有重复元素。
输入:s = "abc"
输出:["abc","acb","bac","bca","cab","cba"]和全排列同样的思路,细节上有点差异。输入的字符串可以是重复的,如何对结果数组去重是个问题。可以使用 Set 这种数据结构代替数组,即可做到不含重复元素。
var permutation = function (s) {
const res = new Set()
const used = {}
const backtrack = (path) => {
if (path.length === s.length) {
return res.add(path)
}
for (let i = 0; i < s.length; i++) {
if(used[i]) continue
used[i] = true
backtrack(path+s[i])
used[i] = false
}
}
backtrack("")
return [...res]
};LeetCode 51. N 皇后
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。
输入:n = 4
输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释:如上图所示,4 皇后问题存在两个不同的解法。皇后彼此不能相互攻击,也就是说:任何两个皇后都不能处于同一条横行、纵行或斜线上。
可以选定行为正方向,依题意可知,每行只能放置一个皇后。
然后我们可以测试当前行的每一列是否是一个有效的放置位置。
设置记录点为所有行都放置好了皇后时,如果递归结束还没有找到可放置的点,就回溯当前已经做出的选择。
function solveNQueens(n) {
const res = [];
const board = new Array(n);
// 初始化 n x n 的棋盘
for (let i = 0; i < n; i++) {
board[i] = new Array(n).fill(".");
}
// 测试 [row][col] 位置能否放置
const isValid = (row, col) => {
for (let i = 0; i < row; i++) {
for (let j = 0; j < n; j++) {
if (
// 发现 queen
board[i][j] == "Q" &&
// 要放置的位置与其他的 queen 同列、对角线
(j == col || i + j == row + col || i - j == row - col)
) {
return false;
}
}
}
return true;
};
const helper = (row) => {
// 找到问题的解,记录下来
if (row == n) {
const stringBoard = board.slice();
for (let i = 0; i < n; i++) {
stringBoard[i] = stringBoard[i].join("");
}
res.push(stringBoard);
return;
}
for (let col = 0; col < n; col++) {
if (isValid(row, col)) {
board[row][col] = "Q";
helper(row + 1);
// 没有出路或者找到解,就回溯选择
board[row][col] = ".";
}
}
};
helper(0);
return res;
}贪心
介绍
思想:对问题求解的时候,总是做出在当前看来是最好的做法。
适用贪心算法的场景:问题能够分解成子问题来解决,子问题的最优解能递推到最终问题的最优解。这种子问题最优解成为最优子结构。
做题环节
LeetCode 5. 最长回文子串
给你一个字符串
s,找到s中最长的回文子串。
输入:s = "babad"
输出:"bab"
解释:"aba" 同样是符合题意的答案。
输入:s = "cbbd"
输出:"bb"
输入:s = "a"
输出:"a"左右双指针遍历,从中心向两端发散比较,在比较的过程中记录最大回文子串时的左右指针位置。
var longestPalindrome = function (s) {
if (s.length < 2) return s
let l = 0
let r = 0
for (let i = 0; i < s.length; i++) {
sub(i, i)
sub(i, i + 1)
}
function sub(m, n) {
while (m >= 0 && n < s.length && s[m] == s[n]) {
m--
n++
}
if (n - m - 1 > r - l - 1) {
l = m
r = n
}
}
return s.slice(l + 1, r)
};LeetCode 3. 无重复字符的最长子串
给定一个字符串
s,请你找出其中不含有重复字符的 最长子串 的长度。
输入: s = "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。
输入: s = "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。
请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。维护一个滑动窗口,在移动同时统计无重复字符的最长子串长度。
var lengthOfLongestSubstring = function (s) {
let map = new Map()
let l = 0;
let r = 0
let res = 0
while (r < s.length) {
// 在当前窗口范围内有重复,则移动左指针
if (map.has(s[r]) && map.get(s[r]) >= l) {
l = map.get(s[r]) + 1
}
res = Math.max(res, r - l + 1)
map.set(s[r], r)
r++
}
return res
};LeetCode 76. 最小覆盖子串
给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 “” 。
注意:
对于 t 中重复字符,我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
如果 s 中存在这样的子串,我们保证它是唯一的答案。
输入:s = "ADOBECODEBANC", t = "ABC"
输出:"BANC"
输入:s = "a", t = "a"
输出:"a"
输入: s = "a", t = "aa"
输出: ""
解释: t 中两个字符 'a' 均应包含在 s 的子串中,
因此没有符合条件的子字符串,返回空字符串。同样是维护一个滑动窗口来遍历字符串,并用字典存储需要的字符数量,在当前滑动窗口内若满足需求,就记录最小长度。同时尝试移动滑动窗口,如果移动后当前滑动窗口不能满足需求,就回溯需求的数量。
var minWindow = function (s, t) {
let need = new Map()
let res = ''
let l = 0
let r = 0
for (let c of t) {
need.set(c, need.has(c) ? need.get(c) + 1 : 1)
}
let needType = need.size
while (r < s.length) {
const c = s[r]
if (need.has(c)) {
need.set(c, need.get(c) - 1)
if (need.get(c) === 0) {
needType -= 1
}
}
while (needType === 0) {
let newRes = s.substring(l, r + 1)
if (!res || res.length > newRes.length) {
res = newRes
}
const c2 = s[l]
// 移动后不能满足需求,回溯
if (need.has(c2)) {
need.set(c2, need.get(c2) + 1)
if (need.get(c2) === 1) { needType += 1 }
}
// 左指针右移,缩小窗口
l++
}
// 右指针右移,扩大窗口
r++
}
return res
};LeetCode 11. 盛最多水的容器
给你 n 个非负整数 a1,a2,…,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) 。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
说明:你不能倾斜容器。
输入:[1,8,6,2,5,4,8,3,7]
输出:49
解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。可以使用左右指针遍历,逐渐收缩容器。观察发现,当其中一边小于另一边时,固定较小的一边,不管如何移动较大的那一边,容器的体积都必定会缩小。因此,每次只移动较小一边的指针,尝试寻找更大的容器体积。
var maxArea = function (height) {
let max = 0
for (let l = 0, r = height.length - 1; l < r;) {
let width = r - l
let minHeight = height[l] < height[r] ? height[l++] : height[r--]
let area = minHeight * width
max = Math.max(max, area)
}
return max
};LeetCode 134. 加油站
在一条环路上有 N 个加油站,其中第 i 个加油站有汽油 gas[i] 升。
你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。
如果你可以绕环路行驶一周,则返回出发时加油站的编号,否则返回 -1。
说明:
如果题目有解,该答案即为唯一答案。
输入数组均为非空数组,且长度相同。
输入数组中的元素均为非负数。
输入:
gas = [1,2,3,4,5]
cost = [3,4,5,1,2]
输出: 3
解释:
从 3 号加油站(索引为 3 处)出发,可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油
开往 4 号加油站,此时油箱有 4 - 1 + 5 = 8 升汽油
开往 0 号加油站,此时油箱有 8 - 2 + 1 = 7 升汽油
开往 1 号加油站,此时油箱有 7 - 3 + 2 = 6 升汽油
开往 2 号加油站,此时油箱有 6 - 4 + 3 = 5 升汽油
开往 3 号加油站,你需要消耗 5 升汽油,正好足够你返回到 3 号加油站。
因此,3 可为起始索引。
输入:
gas = [2,3,4]
cost = [3,4,3]
输出: -1
解释:
你不能从 0 号或 1 号加油站出发,因为没有足够的汽油可以让你行驶到下一个加油站。
我们从 2 号加油站出发,可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油
开往 0 号加油站,此时油箱有 4 - 3 + 2 = 3 升汽油
开往 1 号加油站,此时油箱有 3 - 3 + 3 = 3 升汽油
你无法返回 2 号加油站,因为返程需要消耗 4 升汽油,但是你的油箱只有 3 升汽油。
因此,无论怎样,你都不可能绕环路行驶一周。从全局进行贪心选择,可以把从出发到到达的过程看成是一个整体,如果整个过程中的油量补给小于消耗,那么必定无解。
gasSum += gas[i] - cost[i] ,为每次到达新的加油站前剩下的油量,如果从 0 开始累加到最后还没有变成负数,那么 0 就是合适的起点。
如果累加的最小值是负数,那么途中的所有加油站都不能作为起点,汽车就要从下一个加油站出发,同时 totalSum 就是从 0 开始到当前加油站的油量消耗总和。
继续累加至到达第 n 个加油站,如果中途 gasSum 没有小于 0,并且最终剩下的油量 totalSum 为正数,说明从这个加油站出发,途中能够补给足够的油量来抵消之后的消耗。
var canCompleteCircuit = function (gas, cost) {
let start = 0
let totalSum = 0
let gasSum = 0
for (let i = 0; i < cost.length; i++) {
// 当前油量剩余
gasSum += gas[i] - cost[i]
// 总油量剩余
totalSum += gas[i] - cost[i]
if (gasSum < 0) {
// 去下一点
start = i + 1
gasSum = 0 // 此时的totalSum就变成了这个过程的消耗
}
}
return start > gas.length || totalSum < 0 ? -1 : start
};动态规划
介绍
适用于动态规划的问题,需要满足最优子结构和无后效性,动态规划的求解过程,在于找到状态转移方程,进行自底向上的求解。
做题环节
LeetCode 53. 最大子序和
给定一个整数数组
nums,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
输入:nums = [1]
输出:1用 f(i) 代表以第 i 个数结尾的「连续子数组的最大和」。对于每一个 f(i),其值只与 f(i - 1) 相关,易得出动态转移方程:
f(i)=max{f(i−1)+nums[i],nums[i]}
即可用一个变量来维护当前 f(i) 的值,用一个循环求出所有 f(i)。
const maxSubArray = (nums: number[]): number => {
let prevMaxSum = 0
let maxSum = nums[0]
nums.forEach(num => {
prevMaxSum = Math.max(prevMaxSum + num, num)
maxSum = Math.max(prevMaxSum, maxSum)
})
return maxSum
}LeetCode 673. 最长递增子序列的个数
给定一个未排序的整数数组,找到最长递增子序列的个数。
输入: [1,3,5,4,7]
输出: 2
解释: 有两个最长递增子序列,分别是 [1, 3, 4, 7] 和[1, 3, 5, 7]。
输入: [2,2,2,2,2]
输出: 5
解释: 最长递增子序列的长度是1,并且存在5个子序列的长度为1,因此输出5。可以维护两个数组 dp 和 cnt,分别记录当前递增序列的长度、该长度序列的递增子序列的个数。用 dp[i] 来表示当前递增子序列的个数,易知,长度每次都增加 1。可得动态转移方程:
dp[i] = dp[i - 1] + 1
用 maxLen 记录最大长度,ans 记录最长的个数。当最大长度增加时,ans 需要重置。
var findNumberOfLIS = function(nums) {
let n = nums.length, maxLen = 0, ans = 0;
const dp = new Array(n).fill(0);
const cnt = new Array(n).fill(0);
for (let i = 0; i < n; ++i) {
dp[i] = 1;
cnt[i] = 1;
for (let j = 0; j < i; ++j) {
if (nums[i] > nums[j]) {
// 加上当前元素,就形成新的最大递增序列
if (dp[j] + 1 > dp[i]) {
dp[i] = dp[j] + 1;
cnt[i] = cnt[j]; // 继承之前最长递增子序列的个数
// 是当前的最长递增子序列
} else if (dp[j] + 1 === dp[i]) {
cnt[i] += cnt[j];
}
}
}
if (dp[i] > maxLen) {
maxLen = dp[i];
ans = cnt[i]; // 重置计数
} else if (dp[i] === maxLen) {
ans += cnt[i];
}
}
return ans;
};打印一下 dp 和 cnt,便于理解:
输入:[1,3,5,4,7]
-------dp-------- -------cnt-------
[ 1, 0, 0, 0, 0 ] [ 1, 0, 0, 0, 0 ]
[ 1, 2, 0, 0, 0 ] [ 1, 1, 0, 0, 0 ]
[ 1, 2, 3, 0, 0 ] [ 1, 1, 1, 0, 0 ]
[ 1, 2, 3, 3, 0 ] [ 1, 1, 1, 1, 0 ]
[ 1, 2, 3, 3, 4 ] [ 1, 1, 1, 1, 2 ]- Post link: https://blog.sticla.top/2021/09/25/front-end-interview-review-algorithm/
- Copyright Notice: All articles in this blog are licensed under unless otherwise stated.
GitHub Issues